Nature：量子计算机成功实现监督式机器学习，“杀手级应用”就要来了？

tilldream

目前，机器学习和量子计算的热度可谓不相伯仲，从数学基础上看，二者在某些方面也确实非常相似。

最近，在Nature上发表的一篇论文中，Havlíček等人从二者之间的联系入手，展示了现代量子计算机是如何从数据中进行学习的。论文表明，传统计算机可以将数据映射到只存在量子态的空间中，实现监督式学习。

 

Nature论文：使用量子增强特征空间进行监督式机器学习

地址：https://www.nature.com/articles/s41586-019-0980-2

一提到量子计算机，人们的第一印象往往是，这些机器很难在台式电脑等经典计算机上进行模拟。换句话说，无法使用经典计算机获得量子计算的结果。因为描述量子计算的每个内部步骤需要大量的数字。许多人在学习分割大数字时需要的步骤极其繁多。如果在经典计算机上模拟量子计算，那么每个中间步骤可能需要更多的数字来描述，这个数字甚至可能比宇宙中可观察到的原子总数还要大。

将图像“相似性”概念化为空间距离

由数字集合描述的量子系统的状态被称为量子态。如果量子态与许多数值相关联，则称其在大空间中“存在”。对于某些基于连续变量的量子计算机，这样的空间甚至是无限大的。

 

相比之下，机器学习分析的数据空间要小得多，即用来描述数据的值更少。比如，包含一百万像素的照片仅记录了代表红色、绿色、蓝色的三百万个数字。机器学习的任务目标可能是猜测图像的内容，也可能是生成类似的图像。不过，机器学习中一个成熟的理论称为“核方法”（kernel method），对数据的处理方式与量子理论的数据处理的方式很类似。

 

简而言之，“核方法”是通过定义哪些数据点彼此相似、哪些数据点不相似来执行机器学习任务的。从数学上讲，相似性是数据空间中的距离，即数据点表示之间的距离的数字表示。

目前的假设是，相似的图像具有相似的内容，数据点之间的距离在机器学习中是至关重要的。但对“相似”的确切定义并不像听起来那么简单。比如，如果基于每个图像中的红色像素数量来看，两个图像之间的在数据空间中的距离是多少？

 

数据空间中许多关于“相似性”的定义，在数学上相当于在可能无限大的空间中的相似性的简单量度。因此，在每次比较两个图像时，图像可以被映射到巨大空间中的表示，并计算映射和原图像之间的简单相似性。目前，传统计算机无法确切地计算这个大型表示，但也许量子计算机可以。因为量子计算机能够在极大的空间中进行计算。如果将数据映射到量子态所在的空间，会发生什么呢？

 

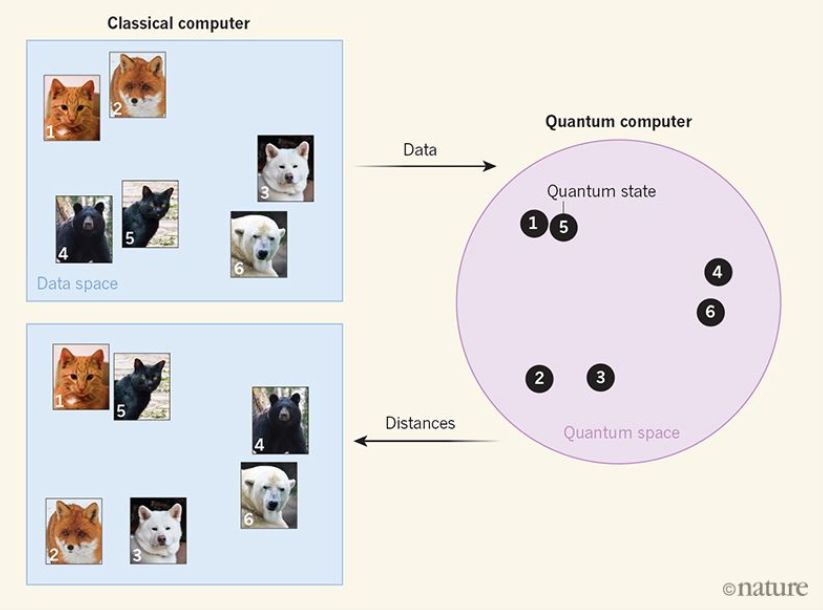
图1 量子增强机器学习过程示意

“量子态”映射反映图像相似性，提升机器学习性能

Havlíček等人展示了量子计算机如何提高机器学习算法的性能。如上图所示，先由传统计算机使用机器学习对动物的图像进行分类。包含相似颜色像素的图像在数据空间中的距离较近。

经典计算机将这些数据发送到量子计算机，后者将每个图像映射到对应量子状态空间中的特定量子态。在数据空间中距离较近、但内容不同的图像，由量子空间中相距很远的状态表示。然后由量子计算机将量子态间的距离发送至经典计算机，改善图像分类效果。

 

Havlíček等人和笔者所在的研究团队几乎同时认识到了机器学习和量子计算之间这种潜在的强大联系。值得注意的是，两个团队提出了基本相同的两种策略，设计用于机器学习的量子算法。第一种策略仅使用量子计算机，作为传统机器学习系统的硬件补充：量子设备在给定两个数据点时返回相似性。第二种策略在量子计算机上进行真正的学习，以经典计算机作为辅助。

 

Havlíček等人的重要贡献是他们在真正的量子计算机上的原理验证实验中实现了这两种策略：他们使用的是IBM的量子芯片。尽管一些新闻报道有些夸张，但任何在云中尝试量子计算的人都知道，由于计算中的实验噪声水平很高，从这些设备中收集有意义的数据是非常困难的。

实验使用的IBM Q量子计算机

在某些人看来，这个实验。量子空间只有四个维度，因为在IBM云服务已经能够提20量子比特设备访问，但这个实验只使用了IBM最小的5量子位芯片的两个量子比特。实验中的数据集同样是人工设计的，让四维空间中的分析过程变得更简单。

 

尽管如此，此文仍然证明了使用量子计算机进行机器学习的革命性方法，并提出了将更流行的人工神经网络融入量子计算领域的多种尝试，“核方法”在机器学习和量子理论之间提供了一座桥，令人耳目一新。不过，发现并承认这座桥的存在只是一个开始。

 

Havlíček等人提出的方法的确切性还有待进一步观察。尽管在量子空间中进行数据表示，对于真实世界的机器学习应用是有用的。不过，我们并不知道该方法是否与有意义的相似性量度相关，比如，在对动物的图像进行分类时，是否可以做到将猫的图片放置在另一幅猫的图片附近，而不是狗的图片附近。

 

此外，目前关于是否存在性能和效果更好其他策略，仍然不是十分清楚。这个技术是否足以战胜已使用了近30年的经典方法？如果可以，量子计算机的“杀手级应用”可能很快就要诞生了。但这无疑是一个更加复杂的问题。

参考链接：

https://www.nature.com/articles/d41586-019-00771-0

论文地址：

https://www.nature.com/articles/s41586-019-0980-2